Условия всех задач из категории B9

На протяжении всего своего существования человечество в своей практической деятельности (научной, образовательной, художественной, технологической, политической и т. п.) постоянно использует, применяет и создает модели окружающего мира. Не существует однозначных и строгих правил построения моделей.

В чем фундаментальный смысл модели? В том, что модель позволяет представить в наглядной визуальной форме объекты и процессы, недоступные для непосредственного восприятия (очень большие или очень маленькие объекты, слишком быстродвигающиеся или, чересчур замедленные процессы и т.п.).

Первые физические модели появились еще в глубокой древности, когда первобытные люди пытались рисовать хищников на песке и пытались пояснить своим сородичам, что данные животные чрезвычайно опасны для жизни.

Информационная модель – модель объекта реального мира, представленная в виде информационного посыла, описывающего существенные для анализа характеристики и параметры рассматриваемого объекта и корреляции между ними.

Схема – представление чего-либо в самых общих чертах, немного вульгарно.

График – множество точек координатной плоскости. Любой график отражает какой-либо процесс или какую-либо зависимость.

Таблица – представление какой-либо информации в ячейках специальной структуры данных, притом с каждой ячейкой можно сопоставить пару значений – номер строки и номер колонки.

Формула – специализированная форма записи некого суждения (детерминированная величина, уравнение, неравенство).

Оптимальный маршрут - маршрут, проделанный исполнителем за оптимальное время, удовлетворяющий всем граничным критериям (как правило, основным граничным критерием выступает минимизация затрат в процессе движения исполнителя по маршруту).

Превалирующее большинство задач из данной категории связано с нахождением оптимального пути между заданными пунктами. Как правило, детерминация пути производится полным перебором всех возможных путей, с отсечением явно неподходящих маршрутов.

Объектный граф - это совокупность узлов (вершин) и ребер (линий), соединяющих эти узлы.
Объектные графы обеспечивают простой способ учета взаимных связей в множестве объектов определенной предметной области.

При визуализации графа необходимо дифференцированно понимать предметную область, которую он будет описывать. Необходимо выделить сущности, которые будут выступать в качестве узлов графа, а также понимать, какие взаимные связи будут определяться между вершинами, и какую количественную оценку эти связи будут выражать.

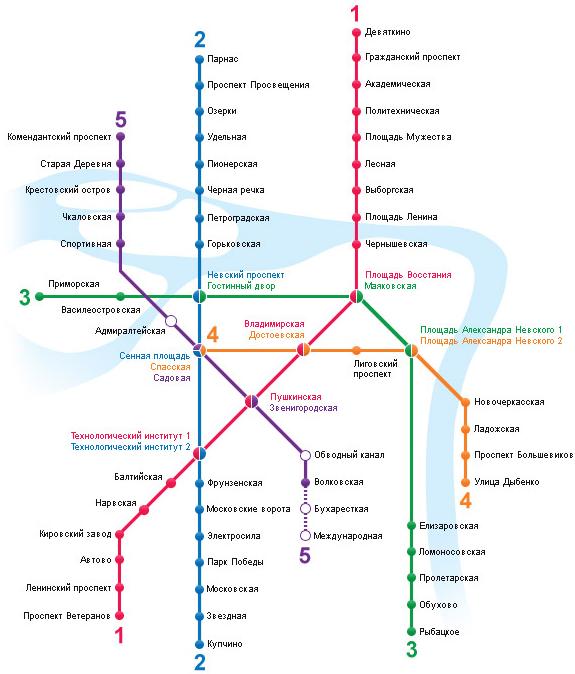
Ярким визуальным примером объектного графа является любая схема метро. Рассмотрим схему петербургского метрополитена. Общее количество станций метро, на сегодняшний день составляет 65 штук. В качестве узлов (или вершин) объектного графа взяты названия станций, в качестве ребер - наличие железной дороги между конкретными станциями. Каждое ребро имеет такую характеристику, как вес. Под весом ребра графа можно понимать, что угодно. В контексте карты метро, разумеется, в качестве веса ребра принимается протяженность, записанная в метрике [метр] (например, между ст. Электросила и ст. Парк Победы протяженность составляет 1213 метров). Можно встретить и другую оценку ребра между станциями метрополитена - продолжительность передвижения, то есть указывается, сколько времени будет затрачено на расстояние между выбранными станциями (например, от ст. Пионерская до ст. Удельная поезд добирается за 2 минуты и 33 секунды).

Для успешного решения задач из данной категории вы должны:

1. разобраться со структурой представленного маршрута, понять взаимосвязи, что собою представляют узлы;

2. детально провести анализ формата отображения графов, предложенных в вариантах ответа;

3. возможно, исключить избыточные траектории, имеющиеся на схеме;

4. определить простым перебором оптимальный маршрут;

5. грамотно применить физическую формулу, связывающую такие величины как: скорость, время и расстояние;

6. привести все рассматриваемые графы к единому формату визуализации (как правило, существует два формата: текстовый и графический) и найти соответствие между заданным графом и одним из предлагаемых графов в варианте ответа.

Дано:
на соревнованиях по спортивному ориентированию участник должен пробежать от старта до финиша, преодолевая наименьшее число препятствий (их число на каждом отрезке пути указано на рисунке).

Найти:
какое наименьшее число препятствий может преодолеть спортсмен?

Дано:
имеется следующее описание графа: a(1,2)  b(1,4)  c(2,4)  d(3,5)  e(4,5)  f(3,4)

Вопрос:
укажите графическое представление описанного в "Дано" графа

Дано:
пятеро мальчиков живут в одном доме: Петр, Александр, Николай, Тимур и Григорий.

• Петр любит кататься с Николаем на скейтборде, а в спортивный зал ходит вместе с Григорием;

• Тимур и Александр обмениваются компьютерными играми;

• Николай ездил в турпоездку вместе с Александром и Тимуром;

• Александр играет в футбол с Тимуром и Петром;

• Григорий ходит в музей с Александром и Николаем.

Вопрос:
кто из мальчиков не поддерживает между собой никаких отношений?

Дано:
из города Жириновск в город Зюгановск можно проехать тремя дорогами:

1. напрямую до города Зюгановск по грунтовой дороге, ее длина 90 км;

2. через поселок Путёный по асфальтовой дороге; от Жириновска до Путёного 90 км, а от Путёного до Зюгановска − 30 км;

3. через поселок Прохоровка; до поселка Прохоровка проложена асфальтовая дорога длиной 90 км, а от Прохоровки до Зюгановска дорога длиной 10 км совсем разбита и требует ремонта.

Также известно, что:

• скорость передвижения по асфальту - 90 км/час;

• скорость передвижения по грунтовой дороге - 60 км/час;

• скорость передвижения по дороге, требующей ремонта - 10 км/час.

Вопрос:
по какой дороге быстрее всего добраться из Жириновска в Зюгановск?